Teacher’s Best Friend: Base-10 Blocks
Primary students are at a special stage of cognitive development where they start maturing from concrete thinking to abstract. Nowhere is this more evident than in mathematics. As your K-1 students move into addition through 10, they will need to relate the concrete to the abstract to transition smoothly.
Using base-10 blocks to represent equations is a great way to provide the conceptual understanding of those equations and demonstrate the strategies for solving them. It builds a much deeper knowledge of addition than just memorizing facts. This more thorough learning, in connection with concrete models, leads to better comprehension and retention of concepts.
Assuming your students understand the basics of place value (check this post for more on that topic), these strategies will help you teach addition through 10 with base-10 blocks. The screenshots below are of the actual online exercises, however, you can also use physical rods and cubes to implement these ideas in your classroom.
All of the exercises mentioned here are part of the HappyNumbers.com course and are presented along with exercises using other representations.
1. Adding and Subtracting with a 10-rod
Before introducing addition or subtraction through 10, it’s a good idea to model several problems that use the number 10. Use written equations and illustrate them with a 10-rod and additional cubes.
Add cubes to the 10-rod:
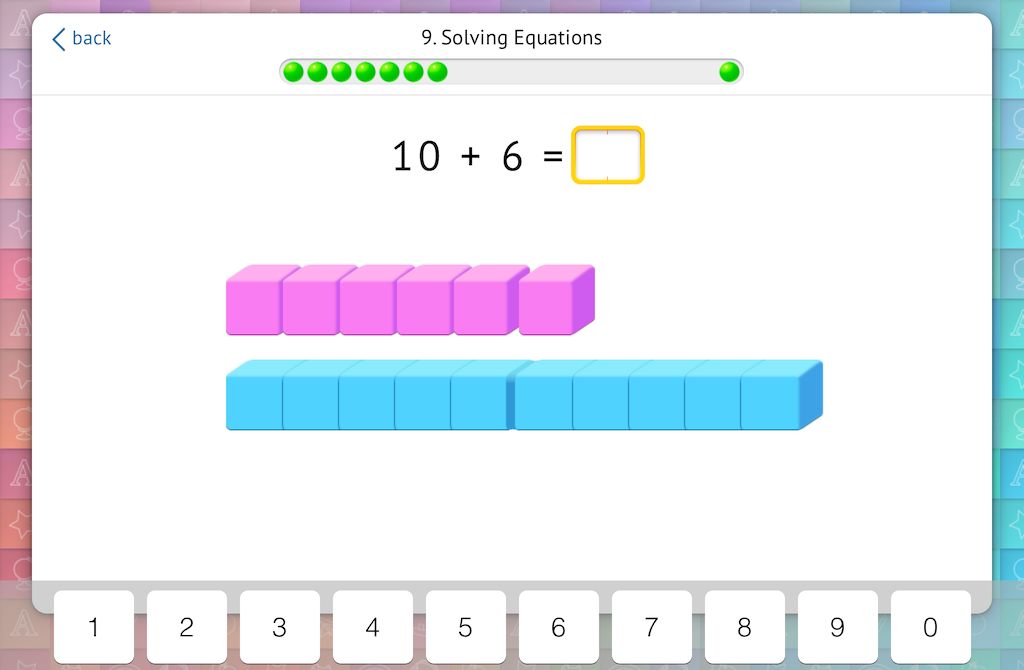
Subtract 10 from a number composed of a 10-rod and cubes:

Or subtract all of the ones:
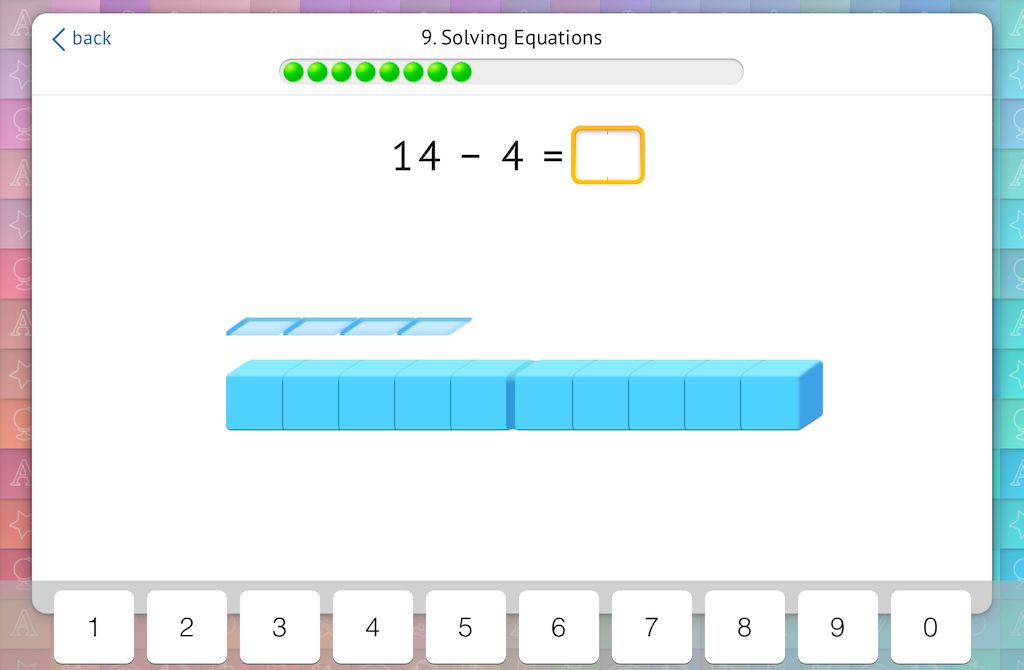
These activities reinforce place value understanding for your students and are a great warm up before progressing further.
2. Missing Addend or Subtrahend
Similar to the previous activities, these exercises work with teen numbers – a combination of a 10-rod and cubes. Rather than adding them together or removing the rod/cubes, however, this time students reverse the logic.
Missing addend problems rely on the understanding of tens and ones to determine how many more cubes are needed:
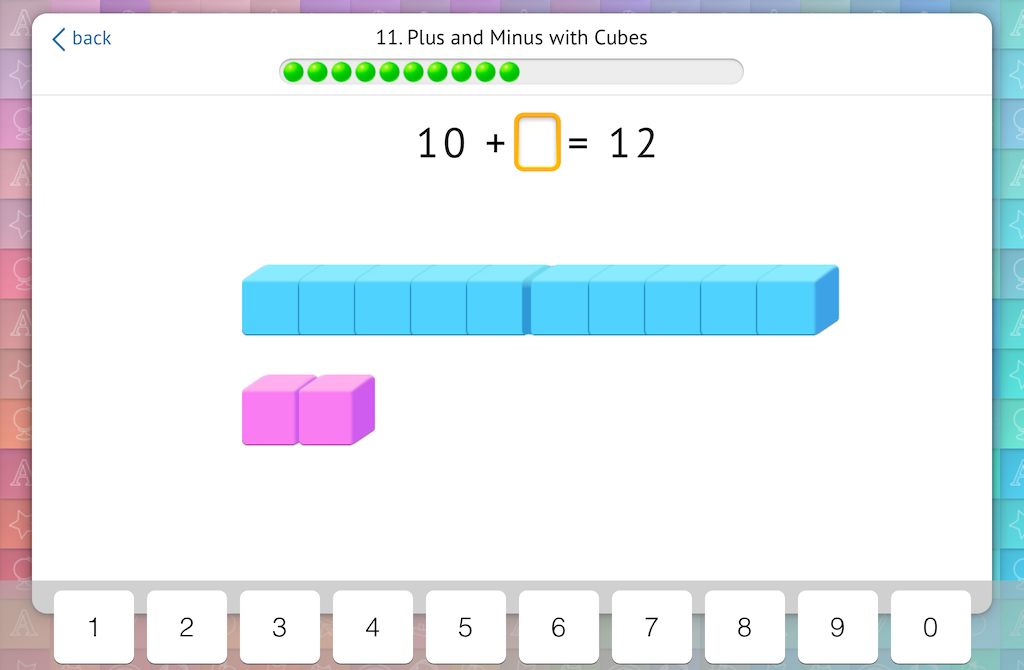
Missing subtrahend problems require similar understanding of breaking a teen number into tens and ones to determine the quantity that was removed:
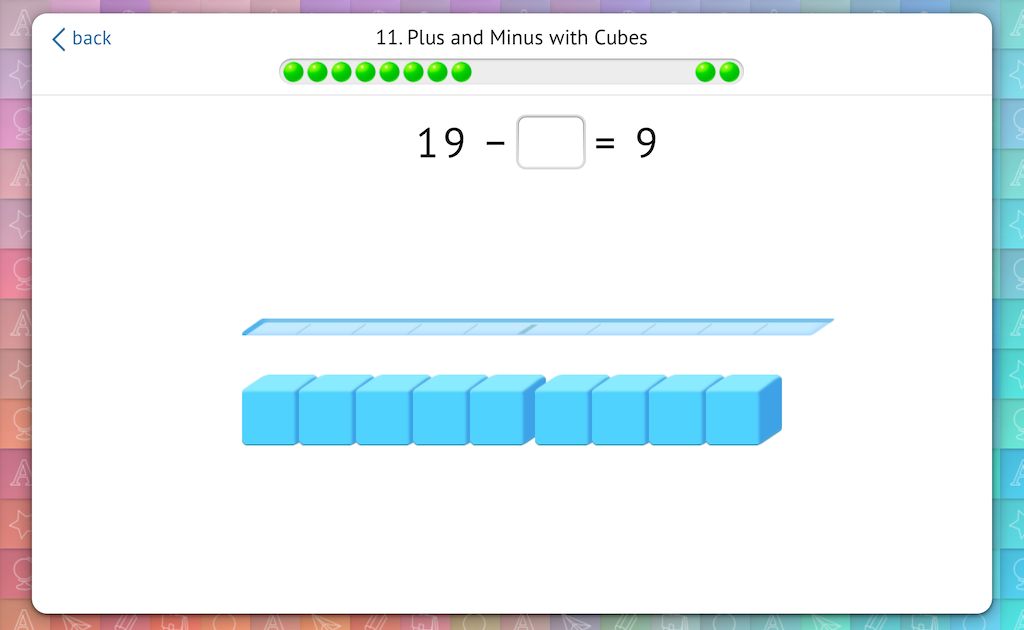
3. Plus/Minus without Transition
As a next step, model addition and subtraction problems without transitioning through 10. Use a written equation and model the numbers using rods and cubes.
For addition, begin with a number in the teens and add cubes (staying within 19):
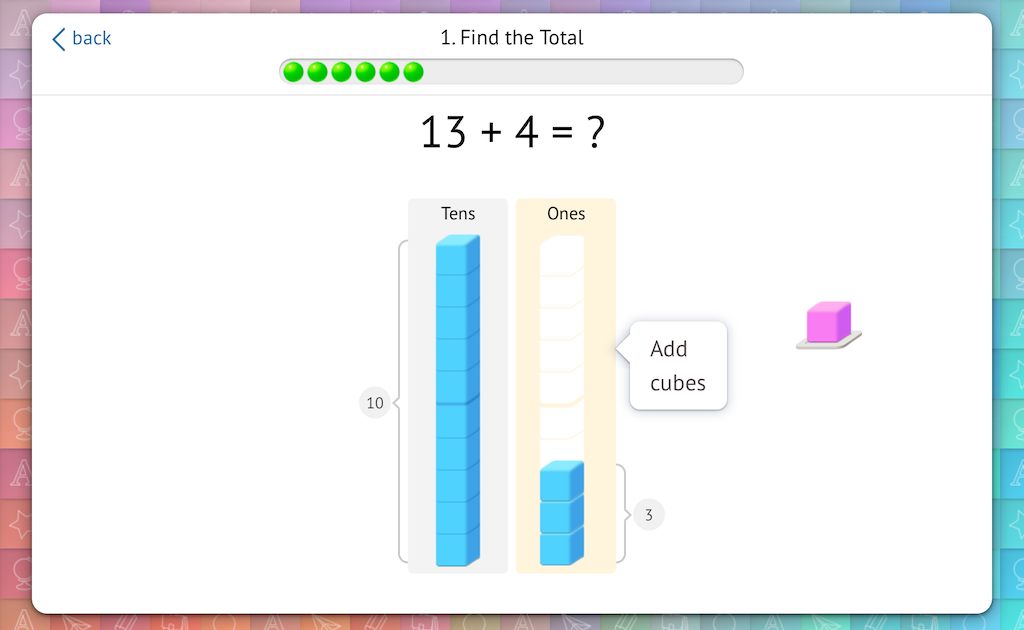
For subtraction, begin with a number in the teens and remove cubes (without going below 10):
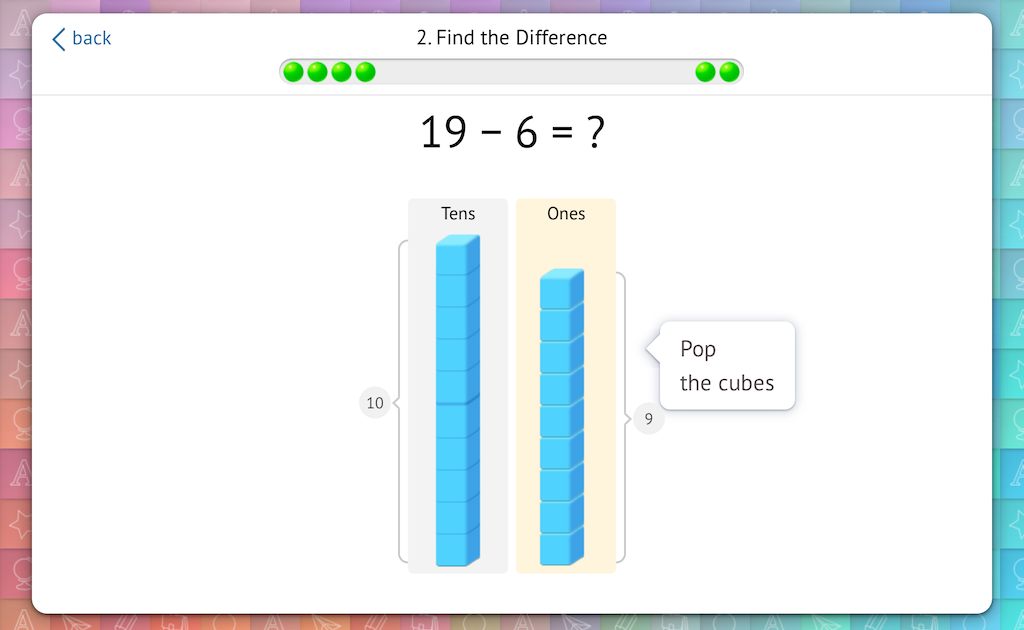
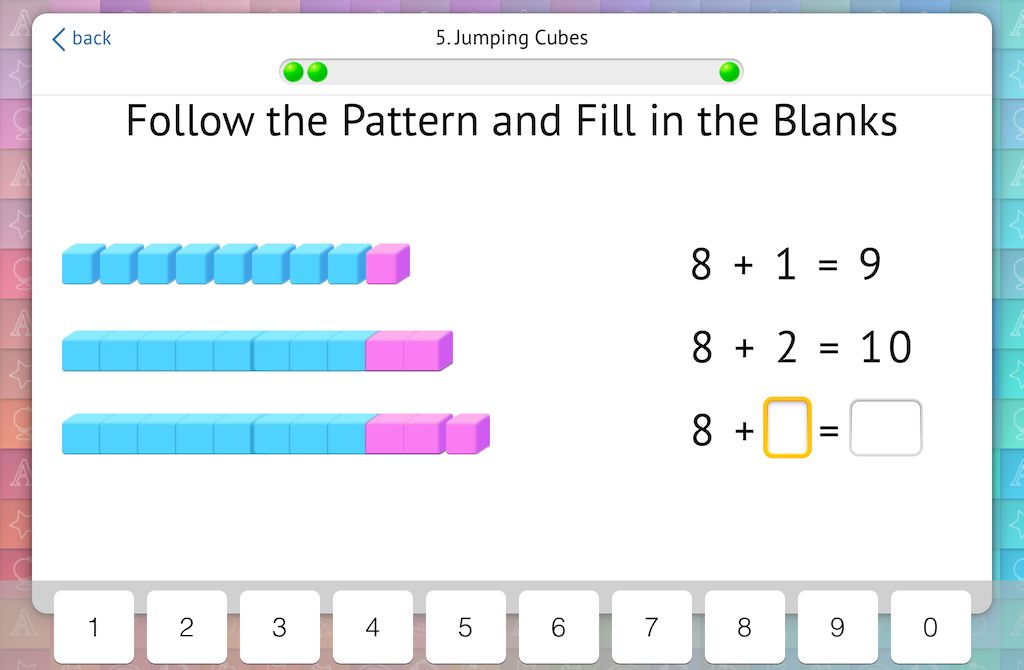
4. Transition through 10, One Cube at a Time
Begin the transition through 10 by systematically adding or removing cubes one by one. The “aha” moment comes when students must exchange their 10 cubes for a rod:
Or break down a rod by exchanging it for 10 cubes:
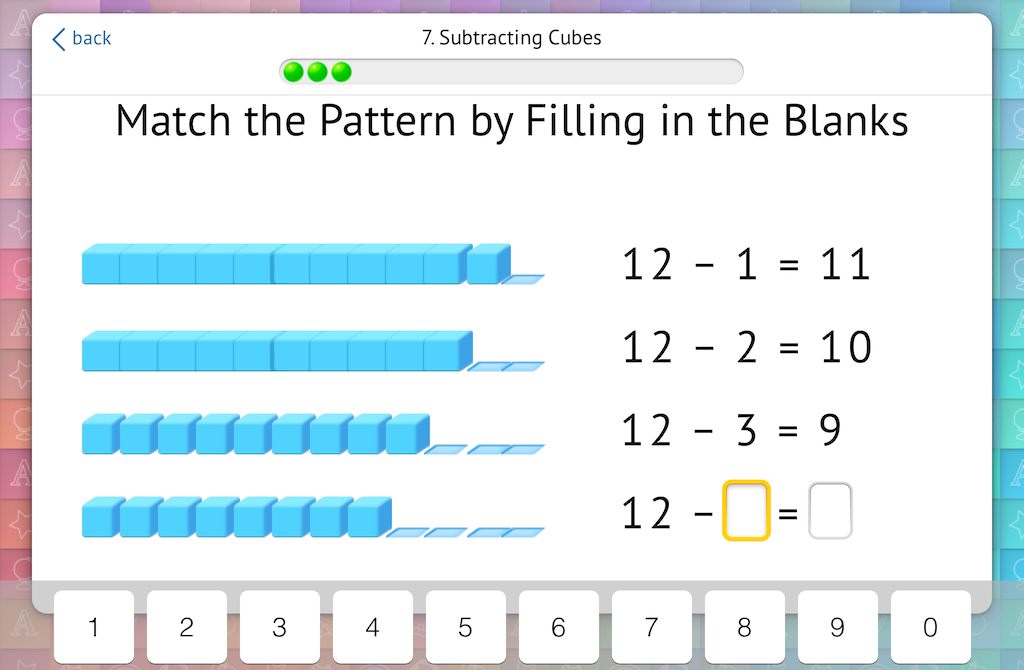
5. Solving Three Addends by Finding 10 First
In this exercise, students learn to think of single-digit numbers as parts of a 10. This will prepare them for future addition and subtraction strategies in which they break numbers in constituent parts.
Here, they add the groups of cubes in a specific order to build a 10 first, then add the remaining cubes:

6. Breaking it Down
One of the most effective mental addition strategies, breaking numbers into parts, allows students to more easily add on to a group of 10. Here, they are forced to complete the Tens column by choosing part of the addend. They then move the remaining part into the Ones column. The result shows that they have added 5 in two parts to arrive at a number comprised of a ten and two ones:
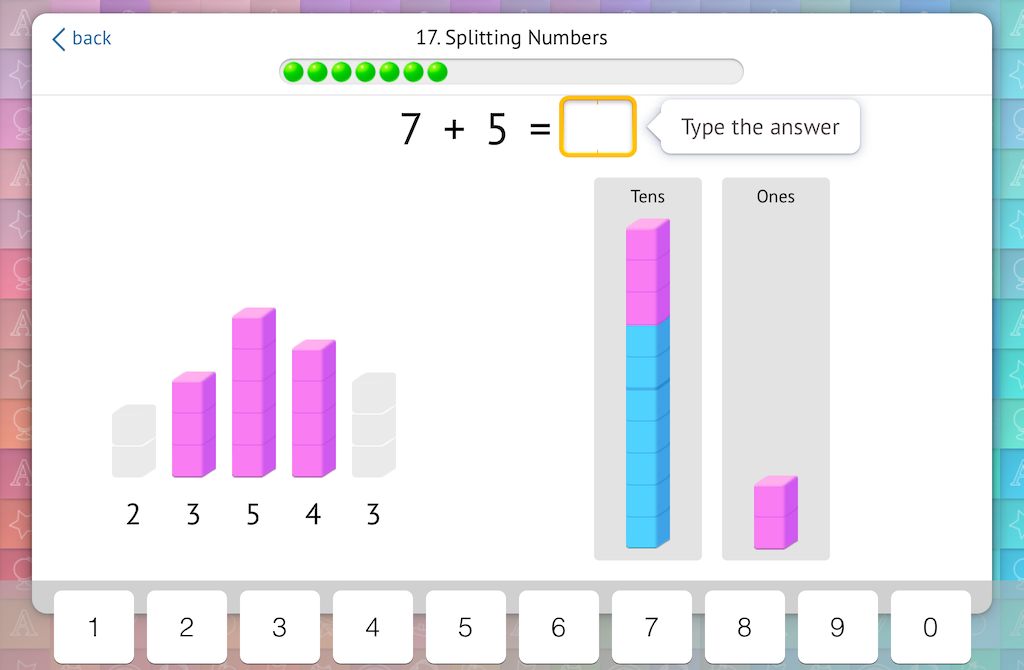
This strategy continues as students break down an addend on their own and relate it to a written equation. Essentially, they are relying on the skill from tip #5 to create a problem with three addends. Therefore, they think of 6+5 as the simpler 6+4+1:
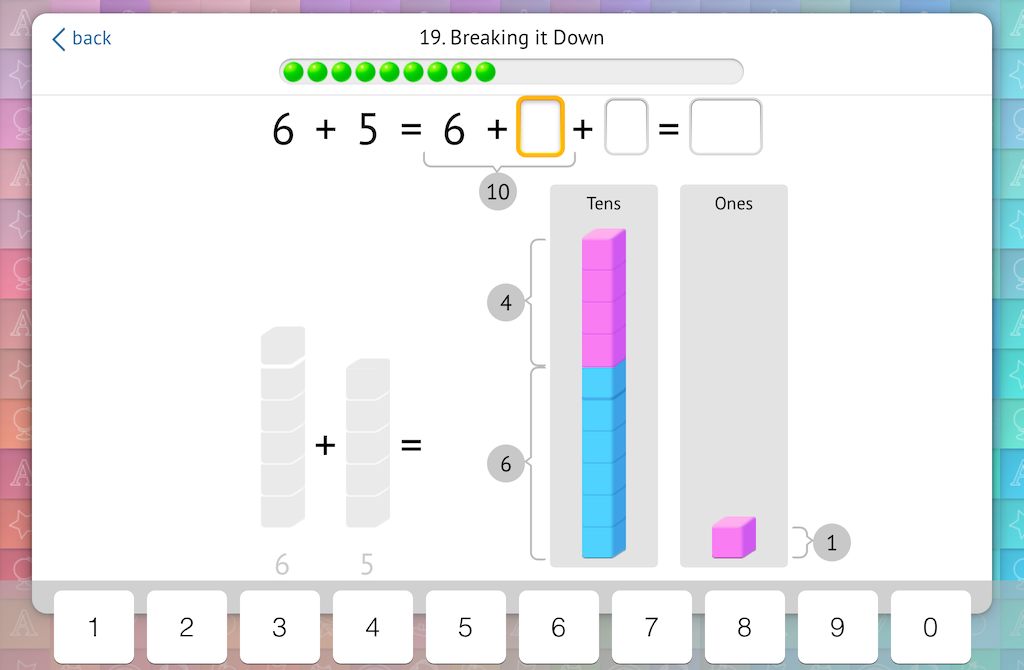
7. Almost 10
Finally, we recommend teaching a strategy for adding ‘almost 10’. By sliding a single cube from one addend to another, students learn to visualize the group of 10 and remaining cubes. Again, they are translating a more difficult addition problem (6+9) to a simpler one (5+10):
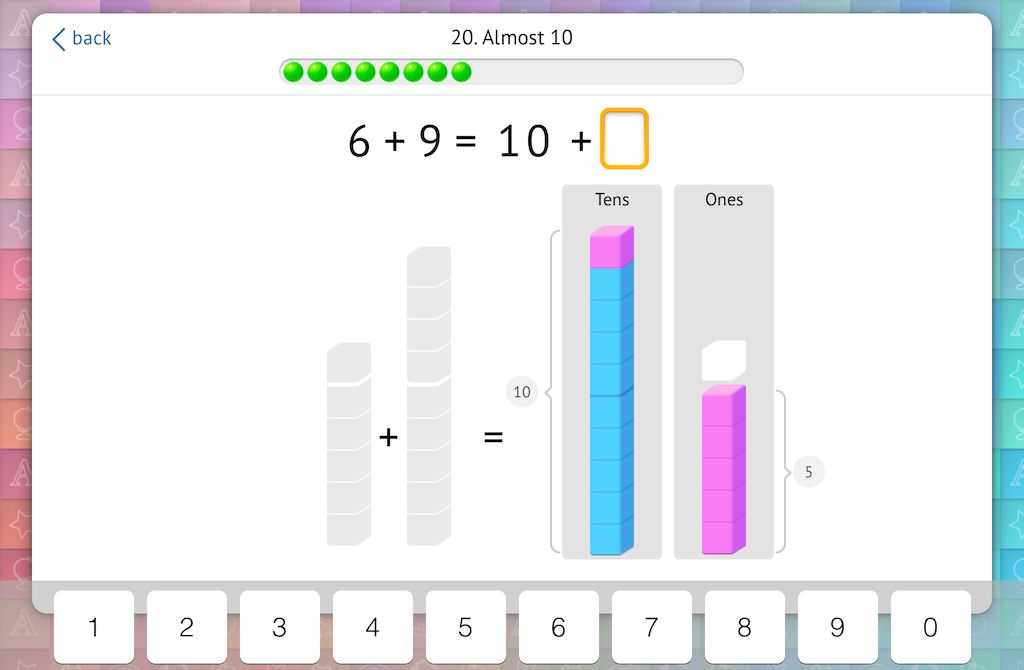
At HappyNumbers.com we have carefully examined each step of learning these early addition and subtraction skills and have planned interactive exercises to help your students master them. Whether you use physical blocks, model our exercises on a smartboard, or have students sign in to their own account to work online, these strategies will ensure success in your classroom.
Check out these exercises and more in your Happy Numbers account.
New to Happy Numbers? Learn more!
Bonus: Using Number Lines
As you can see, base-10 blocks are a great representation of numbers for young learners. They are especially useful at the point of learning to add and subtract through 10. However, once your students progress past that point, base-10 blocks have certain limitations. For example, larger numbers involve a larger number of materials. It is a slow process to represent equations with blocks. You can’t really represent decimals or negative numbers with the blocks.
That’s why it’s important to balance this model with other options. The number line, for example, is another useful model. At Happy Numbers we alternate exercises using base-10 blocks with those using the number line. You can read more here, but for now here are a couple of ideas on how to use a number line to support learning addition through 10.
At first, we model an equation with a number line labeled with all numbers 0-20:
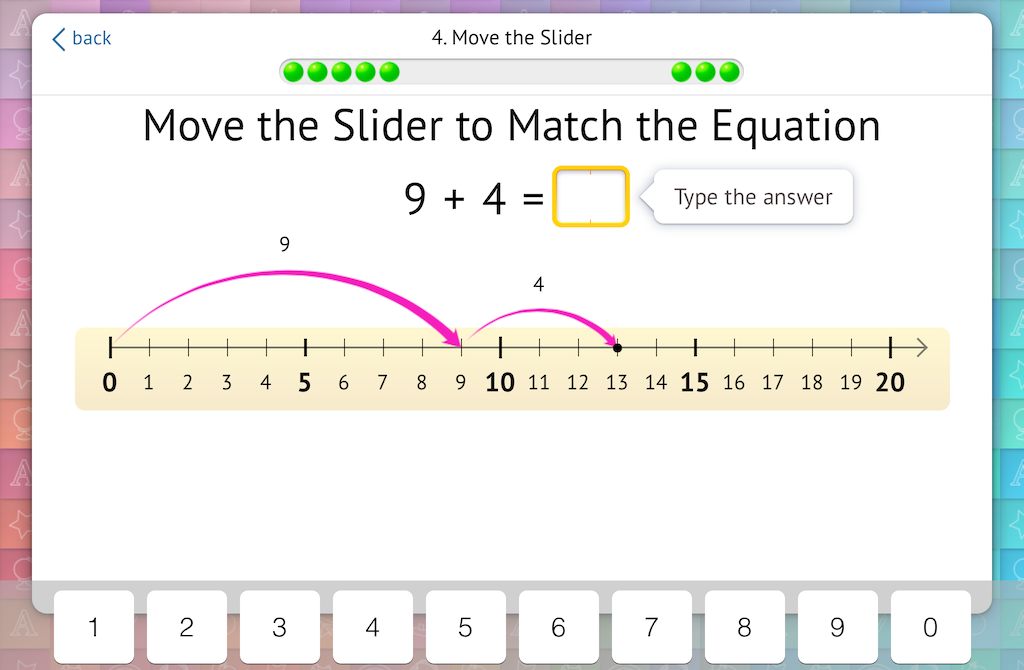
We then increase the complexity by only labeling 0 and 20. As students work through the equation, the other labels appear:

The same strategy applies for subtraction:

—
Yours,
Happy Numbers Team
Yours,
Happy Numbers Team
